Empirically Measuring Concentration: Fundamental Limits to Intrinsic Robustness

Abstract

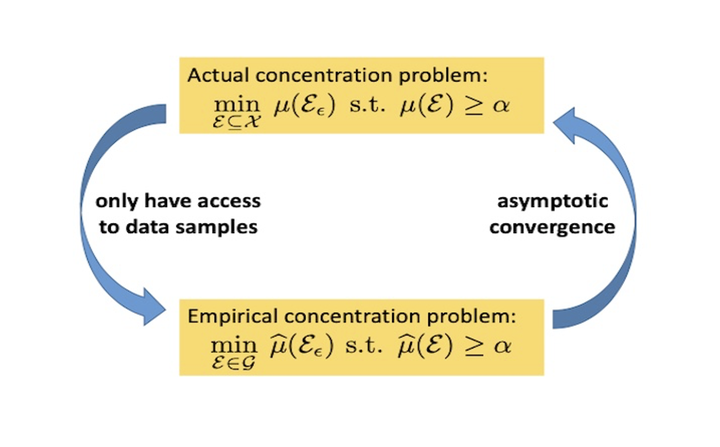
Many recent works have shown that adversarial examples that fool classifiers can be found by minimally perturbing a normal input. Recent theoretical results, starting with Gilmer et al. (2018b), show that if the inputs are drawn from a concentrated metric probability space, then adversarial examples with small perturbation are inevitable. A concentrated space has the property that any subset with Ω(1) (e.g., 1/100) measure, according to the imposed distribution, has small distance to almost all (e.g., 99/100) of the points in the space. It is not clear, however, whether these theoretical results apply to actual distributions such as images. This paper presents a method for empirically measuring and bounding the concentration of a concrete dataset which is proven to converge to the actual concentration. We use it to empirically estimate the intrinsic robustness to l∞ and l2 perturbations of several image classification benchmarks. Code for our experiments is available at https://github.com/xiaozhanguva/Measure-Concentration.