Abstract
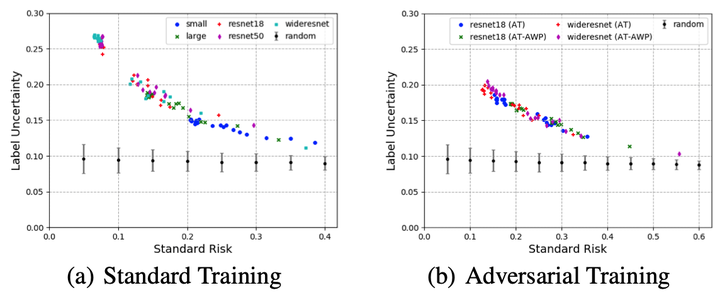
Starting with Gilmer et al. (2018), a line of theoretical works have focused on studying the concentration of measure phenomenon which is fundamentally connected to adversarial robustness. In this work, we argue that the standard concentration is not sufficient to characterize the intrinsic robustness limit for an adversarially robust classification problem since it does not take data labels into account. Built upon on a novel definition of label uncertainty, we empirically demonstrate that error regions induced by various state-of-the-art classification models tend to have much higher label uncertainty than randomly selected subsets. This observation implies that in order to obtain a more accurate intrinsic robustness limit for a particular data distribution, it is important to understand the concentration of measure regarding the input regions with high label uncertainty. In this paper, we adapt the standard concentration problem to produce a more accurate estimate of intrinsic robustness that incorporates label uncertainty and study the error region characteristics of the state-of-the-art machine learning classifiers.