Fast and Sample Efficient Inductive Matrix Completion via Multi-Phase Procrustes Flow

Abstract

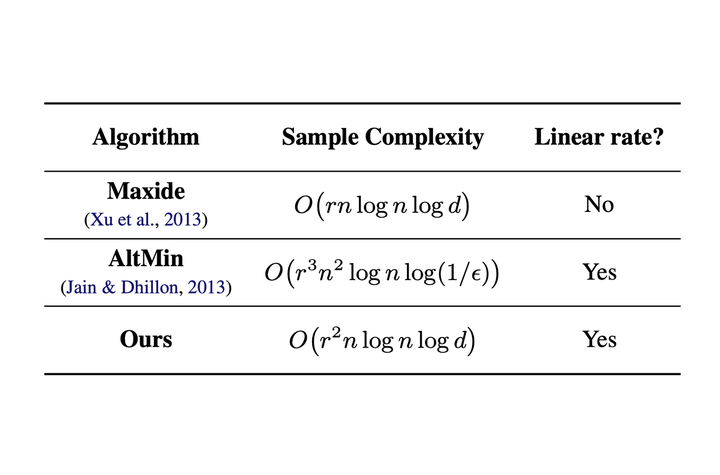
We revisit the inductive matrix completion problem that aims to recover a rank-r matrix with ambient dimension d given n features as the side prior information. The goal is to make use of the known n features to reduce sample and computational complexities. We present and analyze a new gradient-based non-convex optimization algorithm that converges to the true underlying matrix at a linear rate with sample complexity only linearly depending on n and logarithmically depending on d. To the best of our knowledge, all previous algorithms either have a quadratic dependency on the number of features in sample complexity or a sub-linear computational convergence rate. In addition, we provide experiments on both synthetic and real world data to demonstrate the effectiveness of our proposed algorithm.